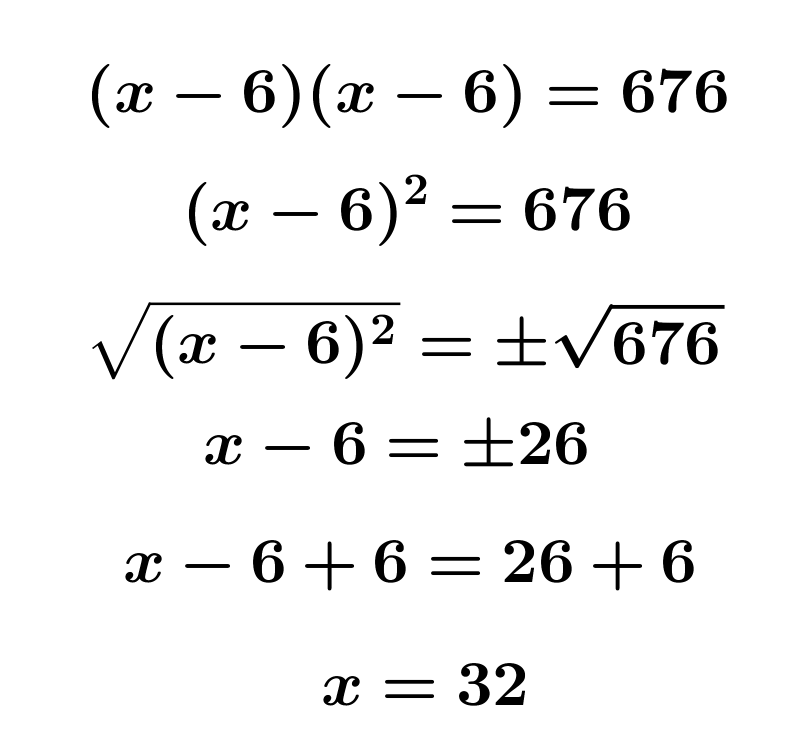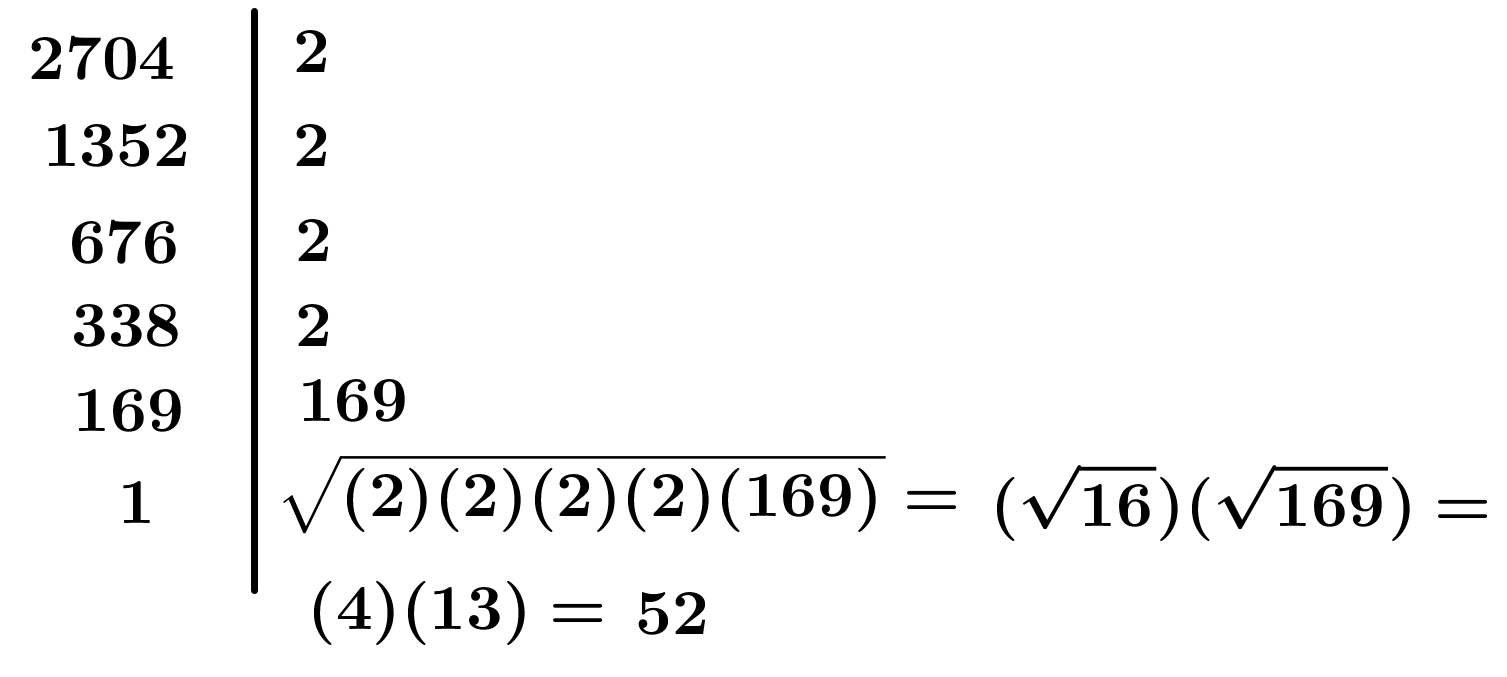São diversos cursos voltado para o ensino de matemática.
quinta-feira, 30 de janeiro de 2014
segunda-feira, 27 de janeiro de 2014
SAIBA PORQUE VOCÊ NÃO LEMBRA COMO RESOLVER UMA EQUAÇÃO DO SEGUNDO GRAU. MALDITO BHASKARA.
Iniciar com um problema recreativo é uma boa forma de diagnosticar habilidades e inabilidades da classe. Eis o problema:
Você tem uma região quadrada de lado desconhecido e que dela foi retirado 3 metros de cada lado sobrando um quadrado menor (óbvio) de 676 m². E então a pergunta, qual o lado do quadrado maior? Vamos resolver de três formas diferentes, a fácil, a fácil e a imbecil.
PRIMEIRA: FÁCIL
Área é um lado vezes o outro, então o lado do quadrado menor é a raiz quadrada de 676 que é 26. Vinte e seis somando 3 metros para direita e 3 metros para a esquerda dá 32. Pronto resolvido, o lado do quadrado maior é 32.
SEGUNDA: FÁCIL
Com uma pequena dose de álgebra, de um lado temos x - 6 do outro a mesma coisa, lado vezes lado igual ao que sobrou, 676 m².
A outra solução da equação não interessa pois não existe medida negativa, -20.
TERCEIRA: IMBECIL
Esta começa já no enunciado, bem característico dos livros didáticos: O prefeito de uma cidade do interior do fim do mundo resolveu criar uma calçada de 3 metros ao redor da praça Santa Maria de Piracema como ilustra a figura a seguir (você já viu a figura neh). Quanto mede CADA lado do quadrado da praça de Santa Maria de Piracema, sabendo que a área criada depois da calçada pronta é de 676 m².(use a fórmula de BHASKARA).
Antes de chegar neste problema você já resolveu 50 exercícios do tipo x² + 2x - 3 = 0 usando a fórmula de BHASKARA, que não é de BHASKARA mentiram pra você. Dez bilhões de anos antes de BHASKARA os chineses já usavam o mesmo método. No mundo inteiro as pessoas falam em fórmula para resolver equações do segundo grau. Mas aqui no Brasil a partir dos anos 60 algum GÊNIO disse que a fórmula é de BHASKARA e deu nisso. E a melhor parte vem agora, a resolução.
Provavelmente você usou um tal de chuverinho, passou para o lado de cá com o sinal trocado, passou pra lá novamente e igualou a zero, separou bonitinho o a, o b e o c, e chegou numa equação do segundo grau, parabéns. O assunto era equação do segundo grau e você desenvolveu umas coisas e chegou, advinha no quê?
Você chegou em uma equação do segundo grau e de quebra identificou a, b e c. Agora é só usar a fórmula de BHASKARA que salta na lousa do nada e além disso, uma fórmula já não é mais uma fórmula, são duas.
Agora é só substituir os valores de a, b e c na fórmula de BHASKARA que não é de BHASKARA e pronto. Ah, primeiro encontre o delta.
E agora um probleminha básico, encontrar a raiz quadrada de delta, na outra fórmula pede isso. Se pode usar calculadora, beleza, se não, você com certeza ouviu a dica: fatore. Então vamos fatorar, não temos calculadora.
Opa 52! Tá terminando...
Pronto, você encontrou 32 como lado do quadrado maior. Com certeza você gastou mais de uma folha, errou pra caramba, desistiu algumas vezes, errou uns 5 sinais, foi mal na prova, o professor foi mau na correção (se tem um sinal errado já era). Na matemática 2 mais 2 é 4 em qualquer lugar do mundo. Dois mais 2 pode ser algo desconhecido. Quanto seria dois carros mais duas cobras? Se você não lembra ou não sabe solucionar uma equação do segundo grau não se preocupe, se você aprendeu da terceira forma é impossível lembrar de tantas coisas desnecessárias. A fórmula da equação do segundo grau só deve ser utilizada quando todos os outros meios de resolução são esgotados. Pesquisei um livro didático de nono ano e listei todas as equações do segundo grau, todas elas sem exceção, não necessita de fórmula pra resolver, são soluções inteiras, sempre. Um meio para resolução é usando uma relação dos coeficientes com as raízes.
 |
Manipulando essa relação podemos usa-la da seguinte forma:
Exemplo. 2x² + 4x -16 = 0, multiplica a vezes c (-32). Troca o sinal do b (-4). Procure dois números que multiplicados dê -32 e somado dê -4. Divida cada um por a (2) e pronto encontrou as duas soluções.
Caso precise do delta, faça 4 - (-8) e eleve ao quadrado, 12², delta igual a 144.
terça-feira, 21 de janeiro de 2014
TRIGONOMETRIA E ACESSIBILIDADE - ABNT NBR 9050
O conteúdo completo deste documento pode ser trabalhado em diferentes séries do Ensino Fundamental e Médio. Nas páginas 41 e 42 sobre o dimensionamento de rampas pode-se elaborar um bom projeto sobre acessibilidade, obedecendo as normas técnicas especificadas no documento.
sábado, 18 de janeiro de 2014
quarta-feira, 15 de janeiro de 2014
terça-feira, 14 de janeiro de 2014
domingo, 12 de janeiro de 2014
GOOGLE DRIVE E DROPBOX
Olá professores de matemática e quem usa o geogebra, se você possui o google drive ou dropbox podemos compartilhar arquivos. Eu tenho disponíveis por exemplo, arquivos do curso de geometria que fiz na PUC em 2011 e estão no google drive caso alguém queira compartilhar é só deixar e mail para adiciona - lo. São atividades como esta, dividir um segmento AB em três partes de igual medida e muitos outros arquivos ggb.
 |
| Este segmento IJ deveria ser AB com as divisões G e H. AG = GH = HB |
quarta-feira, 8 de janeiro de 2014
PROVA DOS NOVE - MULTIPLICAÇÃO
Para verificar se o produto de um número pelo outro está correto existem diversas maneiras, a prova dos 9 pra mim é a mais simples. O proceder é simples e rápido e para a aprendizagem é excelente, multiplicamos, somamos, dividimos e comparamos os restos.
Dois exemplos:
Soma - se a primeira parcela 3 + 3 = 6 e escreva na parte superior esquerda, soma - se a segunda parcela 3 + 1 = 4 e escreva na parte inferior esquerda, multiplique 4 x 6 = 24, 2 + 4 = 6 e escreva na parte superior direita. A soma do resultado obrigatoriamente deve ser 6 ou estará errado. 1 + 0 + 2 + 3 = 6.
Na segunda os mesmos fazeres, se tem 9 nem precisa inclui - lo na soma, dá 7. Se de 79 subtrairmos 9 e 9 e 9 até o final teremos resto 7. A divisão de 79 por 9 tem resto 7 e o melhor caso 7 mais 9 dá 16 e 1 + 6 dá 7 mas como tem o 9 nem precisaria entrar na soma. Continuando 8 + 2 = 10, 1 + 0 = 1, 1 x 7 = 7 e 6 + 4 + 7 + 8 = 25, 2 + 5 = 7.
PROVA DOS NOVES FORA - SUBTRAÇÃO
Na subtração procede-se como se fosse uma soma (224 + 122 e 102 + 467). Primeiro a soma do resultado e do subtraendo, depois o minuendo.
2 + 2 + 4 + 1 + 2 + 2 = 13, 1 + 3 = 4 1 + 0 + 2 + 4 + 6 + 7 = 20, 2 + 0 = 2
3 + 4 + 6 = 13, 1 + 3 = 4 5 + 6 + 9 = 20, 2 + 0 = 2, não precisa somar o nove, daria 11 e 1 + 1 daria 2 da mesma forma.
Usando a congruência módulo m: 224 ÷ 9 tem resto 8, 122 ÷ 9 tem resto 5, somando os restos dá 13 que dividido por 9 deixa resto 4 e 346 ÷ 9 também tem resto 4.
Na segunda: 102 ÷ 9 deixa resto 3, 467 ÷ 9 deixa resto 8, somando os restos dá 11 que dividido por 9 deixa resto 2 e 569 ÷ 9 também deixa resto 2.
segunda-feira, 6 de janeiro de 2014
CONGRUÊNCIA MÓDULO M PARA A 5ª SÉRIE
PROVA DOS 9 OU NOVES FORA
Funciona somando cada número das parcelas e subtraindo 9 toda vez que a soma for maior ou igual a 9. Em seguida faz -se o mesmo com o resultado e os dois números deve ser de igual valor. Exemplo, somando 732 com 421 obtém-se 1153. Somando as duas primeiras parcelas, 7 + 3 = 10 - 9 = 1 + 2 = 3 + 4 = 7 + 2 = 9 - 9 = 0 + 1 = [1]. Para o resultado temos, 1 + 1 = 2 + 5 = 7 + 3 = 10 - 9 = [1]. Valor 1 para as duas somas.
A mesma soma feita direto, 732 + 421 = 1153; 7 + 3 + 2 + 4 + 2 + 1 = 19; 1 + 9 = 10; 1 + 0 = 1; o resultado, 1 + 1 + 5 + 3 = 10; 1 + 0 = 1.
Outro exemplo 72 + 23 = 95, 7 + 2 + 2 + 3 = 14, 1 + 4 = [5]; 9 + 5 = 14, 1 + 4 = [5], obtemos 5 para as parcelas e 5 para o resultado o que indica resultado correto da soma.
A justificativa para a prova dos 9 é a congruência módulo m, que se resume ao seguinte enunciado: dados dois números inteiros a e b, um número m > 0, dizemos que a é congruente a b, módulo m, se e somente se, a dividido m e b dividido por m deixar restos iguais.
Lê-se 12 é congruente a 24 módulo 4, pois 12 dividido por 4 tem resto zero e 24 dividido por 4 também tem resto zero.
Usando o exemplo acima; 732 ÷ 9 tem resto 3, 421 ÷ 9 tem resto 7, somando os retos e dividindo por 9 tem resto [1]. E 1153 ÷ 9 tem resto [1].
Outros exemplos com soma.
Funciona somando cada número das parcelas e subtraindo 9 toda vez que a soma for maior ou igual a 9. Em seguida faz -se o mesmo com o resultado e os dois números deve ser de igual valor. Exemplo, somando 732 com 421 obtém-se 1153. Somando as duas primeiras parcelas, 7 + 3 = 10 - 9 = 1 + 2 = 3 + 4 = 7 + 2 = 9 - 9 = 0 + 1 = [1]. Para o resultado temos, 1 + 1 = 2 + 5 = 7 + 3 = 10 - 9 = [1]. Valor 1 para as duas somas.
A mesma soma feita direto, 732 + 421 = 1153; 7 + 3 + 2 + 4 + 2 + 1 = 19; 1 + 9 = 10; 1 + 0 = 1; o resultado, 1 + 1 + 5 + 3 = 10; 1 + 0 = 1.
Outro exemplo 72 + 23 = 95, 7 + 2 + 2 + 3 = 14, 1 + 4 = [5]; 9 + 5 = 14, 1 + 4 = [5], obtemos 5 para as parcelas e 5 para o resultado o que indica resultado correto da soma.
A justificativa para a prova dos 9 é a congruência módulo m, que se resume ao seguinte enunciado: dados dois números inteiros a e b, um número m > 0, dizemos que a é congruente a b, módulo m, se e somente se, a dividido m e b dividido por m deixar restos iguais.
Lê-se 12 é congruente a 24 módulo 4, pois 12 dividido por 4 tem resto zero e 24 dividido por 4 também tem resto zero.
Usando o exemplo acima; 732 ÷ 9 tem resto 3, 421 ÷ 9 tem resto 7, somando os retos e dividindo por 9 tem resto [1]. E 1153 ÷ 9 tem resto [1].
Outros exemplos com soma.
sexta-feira, 3 de janeiro de 2014
Assinar:
Postagens (Atom)