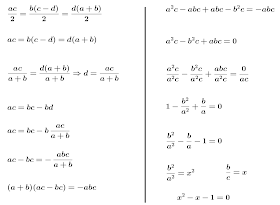ARTE EM ORIGAMI

Excelente!! Confira mais no site da autora Leila Menezes.

POLIEDROS DE CANUDO POR ERNESTO ROSA

PDF ERNESTO ROSA

INTEGRAÇÃO PROFESSORES - ALUNOS

Fase de grupos, terceiro jogo.

POLIEDROS REGULARES: PARTICIPAÇÃO AUMENTANDO

POLIEDROS DOS ALUNOS DO 1º E 2º ANO

Álbum

POLIEDROS DO PRIMEIRO L

ÁLBUM

PADRÕES E CURIOSIDADES NO CÁLCULO DE VOLUMES DE DOIS CILINDROS

Na edição 40 da revista Cálculo, a matéria de capa, DIVISÃO DE CLASSES, traz uma lista com 13 problemas muito interessantes para trabalhar em sala de aula. O problema 4 sugere uma questão relacionado com o volume de dois cilindros feito com a mesma matéria prima, duas folhas de papel A4, um cilindro com 210 mm de altura e o outro com 297 mm de altura. Vale a pena conferir a edição 40 da revista e ver a lista de exercício. Encontrei na internet um arquivo contendo os problemas citados na revista, disponível em:

http://www.uniban.br/institucional/pdf_2014/revista_calculo_maio2014.pdf

O enunciado: Pegue duas folhas de papel A4 e com cada uma delas monte um cilindro; monte um dos cilindros juntando os lados mais compridos de uma das folhas e o outro juntando os lados mais curtos. Cabe a mesma quantidade de arroz nos dois cilindros?

Decidi analisar o problema de outra forma buscando relacionar mais assuntos do ensino médio. Na resolução da revista o aluno imagina como seria se aumentasse a altura e mantivesse o raio e ao contrário também, fiz essa mesma análise só que partindo de dois cilindros iguais de altura 1 e raio 1, obtendo a tabela a seguir:

O volume aumenta muito mais rápido quando o raio cresce e comparando linha por linha, na primeira os volumes são iguais, na segunda aumentou duas vezes, na terceira, três vezes e assim por diante. Ficando evidente qual cilindro caberá mais, o de maior raio.

Para verificar se existe uma relação, raio versus altura, decidi partir de dois cilindros de raio e altura igual a 1 e aumentar uma unidade no raio e uma unidade na altura e igualar os volumes.

Atribuindo valores para h encontramos os valores do raio resolvendo equações do segundo grau. O coeficiente a mantém em -1, o b aumenta de duas em duas unidades e o coeficiente c aumenta de uma em uma unidade. O valor de h sempre será o ponto médio entre as raízes e a distância de uma raiz e a próxima aproxima sempre de duas unidades, o que levou a desconfiar na existência de um limite na distância entre uma raiz e a próxima e um limite na razão do raio com a altura e os dois limites tendendo a 2.

Curiosidades nas raízes: as expansões decimais das raízes são as mesmas para qualquer valor de h e a primeira equação para h igual a 1, tem a mesma expansão decimal da raiz de 2. O número 2 está intimamente ligado a esta relação.

.

E para um h qualquer  -r² + 2rh + h = 0

Padrão dos gráficos

Expansão decimal da raiz de 2

Distância entre uma raiz e a próxima

    applet geogebra

Do lado positivo, a distância entre uma raiz e a próxima tende a 2. Do lado negativo, a raiz seguinte tende a -1/2.

Noção de limite

A hipótese é que dividindo o raio pela altura obtemos 2, isso quando a altura for muito grande. Usando a fórmula de resolução de equação do segundo grau obtemos o valor do raio daí é só dividir pela altura. Recomendo que revise as propriedades de limite.

Resolvendo o limite

Plotando a função obtém se uma hipérbole com assíntota vertical no y e horizontal no 2.

Mova o seletor h (altura)

A tendência é termos sempre um raio com o dobro da altura h mais 0.5, por exemplo para h= 400 teremos raio 800.5, um decimal pouco significativo para h muito grande.


Outra curiosidade é em relação ao volume, quando utilizamos duas folhas de A4 como está na revista, a diferença entre a capacidade de um e de outro fica em torno de 42%. Nesta relação, assim que a altura do cilindro aumenta o raio aumenta duas vezes aproximadamente e a diferença na capacidade de um para o outro diminui consideravelmente chegando a ficar imperceptível quando h  fica muito grande. Por exemplo: quando h=1 o volume é de 18.3 aproximadamente e quando h=2 o volume chega a 124.3 aproximadamente, uma diferença de 579,2%. Para h=40 o volume é de, 813 856 e para h=41 o volume é de 876 172, uma diferença de 7.65%. É claro que 1% de um milhão e 1% 10 tem suas diferenças.

Conferindo no geogebra
digitando essa função no campo de entrada e depois digitando  Limite[ <Função>, <Número> ], Limite[ f, inf ] e enter.

CURSO VEDUCA: EXPLORANDO A GEOMETRIA DAS FORMAS

1. A bela matemática dos corais
2. Ideia + folha de papel = origami
3. Fractais africanos
4. Fractais e a arte da imperfeição
5. Como o cálculo está mudando a arquitetura
6. Simetria, o enigma da realidade
7. A teoria do todo

DISSERTAÇÕES DE MESTRADO SOBRE O USO DE DOBRADURAS PARA O ENSINO DE GEOMETRIA

DISSERTAÇÃO DE LISBOA

DISSERTAÇÃO DO CEARÁ

PIRÂMIDE 2ºA -

Clique com o botão direito e deixe girar

POLIEDROS REGULARES - SEGUNDO ANO A

Pessoal do segundo ano, participem do grupo DOBRADURAS no facebook, a participação por lá será fundamental para as próximas atividades.
Baixem para suas máquinas o programa POLY (Poly 1.12 e clique em Windows)

EQUIVALÊNCIA ENTRE ÁREAS

Equivalência entre as áreas formadas a partir de um triângulo BCD.
arquivo.ggb 1
arquivo.ggb 2
arquivo.ggb 3
arquivo.ggb 4

SITES, GRUPOS E CURSOS QUE FALAM DE GEOGEBRA

Grupos no face:

O GEOGEBRA - Sérgio Dantas
GEOGEBRA BRASIL - Humberto Bortolossi

SITES

O GEOGEBRA
GEOGEBRA
INSTITUTO GEOGEBRA RIO DE JANEIRO
INSTITUTO GEOGEBRA SÃO PAULO
REVISTA DO INSTITUTO GEOGEBRA INTERNACIONAL DE SÃO PAULO

VÍDEOS

GEOGEBRA TUBE
LCMAquino 

QUANTOS ÂNGULOS RETOS TEM NA SUA CASA? SAIBA COMO ELES FUNCIONAM NA MATEMÁTICA

Como seria uma casa construída sem ângulos retos?

Os ângulos retos estão espalhados em todo lugar  e se você destinar um minuto para contar os que tem na sua casa irá perder as contas bem rápido. Toda a estrutura de uma casa qualquer não seria a mesma sem os ângulos retos bem como a matemática não seria a mesma sem os ângulos retos. Uma infinidade de demonstrações deriva de ângulos retos, não dá pra imaginar a matemática sem eles. Se construirmos um ângulo reto e duas paralelas, uma na vertical e outra na horizontal obtemos um retângulo e dividindo-o ao meio pelas diagonais obtemos dois triângulos retângulos. E se dividirmos um quadrado ao meio pelas diagonais? Obtemos dois triângulos quadrados? Não seria errado dizer que sim, mas como todo quadrado é um retângulo, melhor continuar com os triângulos retângulos mesmos.

Construindo ângulos retos com o geogebra.

Crie um segmento AB

Trace uma circunferência de raio AB e centro C

Crie um ponto D sobre a circunferência

Trace uma circunferência com centro em D

Marque a interseção das circunferências, E e F

Trace duas retas, CD e EF

Reta b e reta e são perpendiculares

Crie uma circunferência de centro A e marque um ponto B na circunferência

Crie um segmento AB

Crie outra circunferência de raio AB com centro em B

Marque a intersecção C das circunferências c e d nas parte superior do segmento AB

Trace outra circunferência (e) de raio AB com centro em C

Marque a intersecção D das circunferências d e e 

Trace outra circunferência (f) com centro em D

Marque a intersecção E de e e f

Trace um segmento EB

O ângulo EBA é reto

Retas Perpendiculares

O que são retas perpendiculares? São retas que formam ângulos retos.

O que são ângulos retos? São ângulos formados por retas perpendiculares.

As retas perpendiculares são mais que redundâncias.

As retas perpendiculares é um caso especial de retas concorrentes, tão especiais, tão especiais que são as únicas retas que formam dois pares de ângulos retos. E tem mais, quando estas retas estão no plano, sua análise angular também é única. O coeficiente angular de uma é o oposto do inverso da outra.

Por exemplo, nas funções 2x + 1 = f (x) e -1/2x + 5 = f (x), uma com coeficiente 2 outra com coeficiente oposto e inverso do primeiro. Este fato faz a interseção das duas funções formarem um ângulo reto.

Applet geogebra
Movimente os seletores a, b e c

Para demonstrar o fato acima chegamos nas TRANSFORMAÇÕES TRIGONOMÉTRICAS,
(O baricentro da Mente, bela demonstração) mas não antes de provar algo mais simples como o ângulo externo de triângulo.

Outro teorema onde o ângulo reto está envolvido, o das bissetrizes.

Visualização - paralelogramo com um ângulo reto
Movimente o ponto D ou E

Dadas duas retas paralelas r e s e uma outra reta t transversal a estas duas, as bissetrizes dos ângulos colaterais internos formam um ângulo reto.

E o que seria de Pitágoras sem ângulos retos

DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS, COMPARANDO A ÁREA DO TRAPÉZIO COM AS ÁREAS DOS TRÊS TRIÂNGULOS.

São muitas as possibilidades de falar de algo aparentemente tão simples, mas que desencadeia uma série de fatos fundamentais para a matemática.

SIMETRIAS

ÁREAS TRIANGULARES

A área de um triângulo qualquer pode ser calculada por pelo menos 4 formas diferentes. A mais usual é a base vezes a altura, usada geralmente nos triângulos retângulos. Por determinantes, na geometria analítica onde precisamos das coordenadas ( no exemplo abaixo (2,6), (2,2) e (5,2)). Por semi perímetro, que é a soma dos três lados dividido por 2. Chamado de p, fazemos a raiz quadrada de p vezes p - a vezes p - b vezes p - c, a, b e c são os lados do triângulo. E usando o seno, conhecendo dois lados e o ângulo formado por eles. Usei o triângulo mais manjado da história para facilitar os testes.

A HISTÓRIA DA ELETRECIDADE

GEOMETRIC NEON LIGHT - DANIEL MENTRARD

PRISMA E ANTIPRISMA

Em breve disponibilizarei o tutorial para o "multi tetraedro vazado", square antiprisma e do maior, que ainda não sei o nome.

TFT - TEOREMA FUNDAMENTAL DA TRIGONOMETRIA

DANIEL MENTRARD, O REI DO GEOGEBRA

Pense em qualquer coisa. Agora pense nesta coisa e o geogebra. Agora acessa o site que você vai encontrar.

CANAL NO YOU TUBE - SITE

FEIRA DE MATEMÁTICA IME USP - FEIRA DE CIÊNCIAS

NEUROCIÊNCIA E MATEMÁTICA

Mais uma apresentação do Seminário de Coisas Legais no ICMC-USP
O Andrés Anibal Rieznik (Laboratory of Integrative Neuroscience, Physics Department, University of Buenos Aires) apresendou o seguinte seminário:

A mente humana é o objeto de estudo das ciências cognitivas, mas o seu entendimento e manipulação é a especialidade dos ilusionistas. Nos últimos anos houve um florescimento da interação entre cientistas e mágicos. Como fruto desta colaboração, novos e interessantes descobrimentos sobre o funcionamento do cérebro foram feitos. No Laboratório de Neurociência Integrativa da Universidade de Buenos Aires nos interessamos particularmente pela questão do livre arbítrio. Os mágicos são especialistas em fazer-nos crer que fomos livres numa escolha quando eles, na verdade, nos manipularam psicologicamente para fazer-la. Estudando este fenômeno, conseguimos demonstrar que a dilatação das pupilas de um sujeito pode nos informar, não somente qual escolha foi feita, mas também se o sujeito sentiu-se livre na escolha (ou não). Vou apresentar este estudo nesta palestra.

Além disso, irei fazer uma performance de "matemágica", uma demonstração de atletismo mental que venho fazendo em Buenos Aires como show em um teatro para 600 pessoas seis vezes por semana.

(Seminário de Coisas Legais, You Tube)

AGULHAS DE BUFFON - CÁLCULO PARA O VALOR DE PI USANDO PROBABILIDADE - FEIRA DE CIÊNCIAS

AGULHAS DE BUFFON 1
AGULHAS DE BUFFON 2

EXPERIÊNCIAS MATEMÁTICAS - FEIRA DE CIÊNCIAS

CICLÓIDE




FENÔMENOS ESTROBOSCÓPIOS





ESPIRÓGRAFO - CICLÓIDE





FITA DE MOEBIUS





CATENÁRIA





NÚMEROS PRIMOS





DISTRIBUIÇÃO NORMAL DE PROBABILIDADES

EXPERIÊNCIAS DE BIOLOGIA - FEIRA DE CIÊNCIAS

VÁRIAS EXPERIÊNCIAS DE BIOLOGIA: O LABORATÓRIO DA BIBI

CINQUENTA EXPERIMENTOS DE QUÍMICA - FEIRAS DE CIÊNCIAS

CINQUENTA EXPERIMENTOS DE QUÍMICA

EXPERIMENTOS DE FÍSICA - FEIRA DE CIÊNCIAS

Experimentos disponíveis no site da UNESP, disponível na aba esquerda, guia áreas.

MECÂNICA ÓPTICA ELETRICIDADE E MAGNETISMO FÍSICA TÉRMICA

A TEORIA QUE PREMIOU ARTUR ÁVILA COM O PRÊMIO NOBEL DE MATEMÁTICA

A teoria que já alguns tempos vem premiando matemáticos brasileiros agora coroou Artur Ávila com a Medalha Fields. Prêmio este muito mais difícil de conquistar comparado ao prêmio Nobel. A Medalha Fields contempla de quatro em quatro anos, matemáticos com menos de 40 anos com trabalhos significativos desta Ciência. Abaixo na playlist, a teoria em 10 capítulos, explicando  bem o que é o caos.

   

CORREÇÃO GRÁFICOS SEGUNDO GRAU 3º F/G

LINK DO ARQUIVO PARÁBOLA X CATENÁRIA   HISTÓRIA E APLICAÇÕES

ANÁLISE GRÁFICA FUNÇÃO POLINOMIAL SEGUNDO GRAU

Movimente os seletores a, b, c. Os seletores são os coeficientes e a análise deles irão determinar o tipo do gráfico. Primeiro o delta, se maior que zero, tem duas raízes, se igual a zero, raiz dupla e se menor que zero não tem raízes. Coeficiente a determina a concavidade da parábola, se positivo, para cima, se negativo para baixo. O coeficiente b determina a passagem da parábola no eixo y. Se b for positivo a parábola passará subindo e se b for negativo a parábola passará descendo, sempre observando da esquerda para a direita. O coeficiente c determina onde a parábola passará no eixo y. O encontro da parábola com o eixo x são as raízes (solução, os zeros da função) e o ponto vermelho é o vértice da parábola.

APRENDA A CRIAR A CURVA DA CICLÓIDE NO GEOGEBRA

PROPRIEDADES DA CICLÓIDE, E O SEU SURGIMENTO

Na etapa criar um ponto a(t) A não precisa digitar a letra A, ela já se nomeará como A. O mesmo na etapa criar outros dois pontos, não precisa digitar O e nem R, eles serão nomeados automaticamente como B e C. E por último na etapa criar uma circunferência com centro em A passando por O e R, desconsidere e crie a circunferência com centro em B passando por A e C.

Lembrando que a última versão do geogebra não há a necessidade de digitar o asterisco para a multiplicação e nem dá espaço, no ponto O e R nas etapas da foto é só digitar ( rt,r) ou seja r vezes t vírgula e r e no outro ponto r vezes t vírgula e zero.

Depois de pronto para melhorar a sensação de que a circunferência está girando, clique com o botão direito do mouse, propriedades e mude a cor da curva paramétrica e o mesmo com o ponto A. Em seguida desmarque o ponto C na janela de álgebra. Com o direito novamente clique na circunferência e em exibir rótulo e o mesmo com o ponto B. Por fim movimente ou anime os seletores.

A circunferência não gira...

EXERCÍCIO DE OURO

Qual será a localização exata de N e M para que os três triângulos tenham áreas iguais? Movimente os pontos e tente encontrar

Esse é mais um daqueles problemas que só quem ama matemática consegue ver a beleza  que existe, nem tanto pelo problema mas sim na elegância da resposta.

Quando calculamos a áreas de cada triângulo e igualamos os três chega em um certo ponto que a medida de cada segmento não tem muita importância e sim a razão entre eles.

Na demonstração a seguir, multipliquei tudo por 2 para eliminar o denominador 2, depois encontrei o valor d para diminuir um pouco as variáveis. Encontrei o valor de d do terceiro triângulo e substituir no segundo. Um pouco mais a frente dividir tudo por a²c encontrando duas razão e 1 em uma equação do segundo grau. Em seguida multipliquei tudo por -1 chegando em,  b²/a² - b/a - 1 = 0 o que diferencia em pouco se fosse 

- b²/a² + b/a + 1 = 0, só a concavidade, mas os valores são os mesmos. E para facilitar os cálculos disse que a primeira razão era x² e a segunda x.

Independente da concavidade os valores das raízes são os mesmos. O que sei com esse número é que b/a tem de ser 1.618033... e sabemos que esse número é o famoso phi, o número de ouro ou seja para sabermos onde deve estar o ponto P no enunciado acima basta dividir o segmento BC em extrema e média razão. Procedendo da mesma forma chegaremos a mesma conclusão no segmento CD.

Como dividir um segmento na razão áurea.

Digite no campo de entrada N=P e M=P'

NÚMERO Phi NO TRIÂNGULO ISÓSCELE

Os únicos requisitos são os ângulos da base, 72°.