Qual será a localização exata de N e M para que os três triângulos tenham áreas iguais? Movimente os pontos e tente encontrar
Esse é mais um daqueles problemas que só quem ama matemática consegue ver a beleza que existe, nem tanto pelo problema mas sim na elegância da resposta.
Quando calculamos a áreas de cada triângulo e igualamos os três chega em um certo ponto que a medida de cada segmento não tem muita importância e sim a razão entre eles.
Na demonstração a seguir, multipliquei tudo por 2 para eliminar o denominador 2, depois encontrei o valor d para diminuir um pouco as variáveis. Encontrei o valor de d do terceiro triângulo e substituir no segundo. Um pouco mais a frente dividir tudo por a²c encontrando duas razão e 1 em uma equação do segundo grau. Em seguida multipliquei tudo por -1 chegando em, b²/a² - b/a - 1 = 0 o que diferencia em pouco se fosse
- b²/a² + b/a + 1 = 0, só a concavidade, mas os valores são os mesmos. E para facilitar os cálculos disse que a primeira razão era x² e a segunda x.
Independente da concavidade os valores das raízes são os mesmos. O que sei com esse número é que b/a tem de ser 1.618033... e sabemos que esse número é o famoso phi, o número de ouro ou seja para sabermos onde deve estar o ponto P no enunciado acima basta dividir o segmento BC em extrema e média razão. Procedendo da mesma forma chegaremos a mesma conclusão no segmento CD.
Como dividir um segmento na razão áurea.
Digite no campo de entrada N=P e M=P'


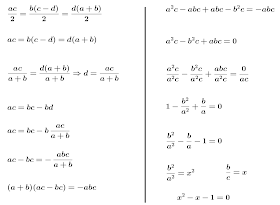



Nenhum comentário:
Postar um comentário
Obrigado pela visita!